Công thức tính diện tích hình phẳng là gì? Để hoàn toàn có thể hiểu hơn về bí quyết tính diện tích hình phẳng và có thể áp dụng vào làm bài bác tập một cách xuất sắc nhất. Vậy thì ngay dưới đây hãy thuộc với chúng tôi đi tò mò trong bài viết sau đây của bọn chúng tôi.
Bạn đang xem: Diện tích hình phẳng giới hạn bởi đồ thị hàm số
Công thức tính diện tích hình phẳng là gì?
– Trong cuộc sống thực tiễn cũng giống như khoa học kĩ thuật thì họ cần cần tính diện tích của không ít hình phẳng phức hợp mà những công thức thông thường không thể thống kê giám sát được.
Ví dụ: diện tích s của mặt hồ tự nhiên, thiết diện cắt ngang của một dòng sông… chính vì như vậy ta cần vận dụng tích phân để hoàn toàn có thể tính được diện tích của rất nhiều hình phức tạp đó.
Xem thêm: Hướng Dẫn Giải Bài Tập Hóa Học 8 Sgk Môn Hóa Học Lớp 8, Giải Bài Tập Hóa Học 8 Trang 11
Diện tích hình phẳng số lượng giới hạn bởi vật dụng thị hàm số và những trục tọa độ
– ví như hàm số y=ƒ(x) liên tục bên trên đoạn
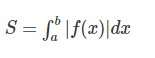
Ví dụ: Tính diện tích S của hình phẳng giới hạn bởi đồ dùng thị hàm số y= x3−x , đường thẳng x=2, trục tung và trục hoành
Cách giải:
-Vì trục tung gồm phương trình tọa độ là x=0 nên áp dụng công thức nêu bên trên ta có :
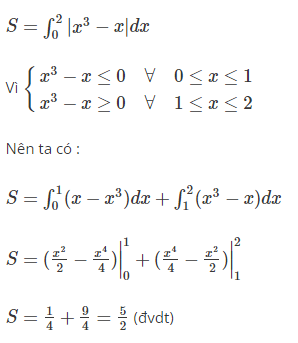
Công thức bao quát tính diện tích s hình phẳng số lượng giới hạn bởi thiết bị thị
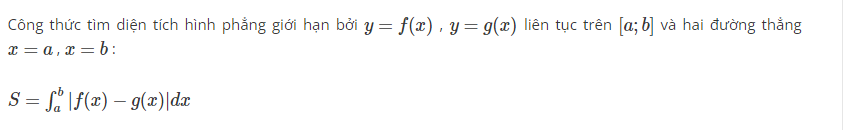
Ví dụ:
Tìm diện tích hình phẳng S được giới hạn bởi thiết bị thị nhị hàm số y= x2+2 và y=3x
Cách giải:
Đầu tiên, ta đã hoành độ giao điểm của nhì hàm số trên bằng cách giải phương trình :
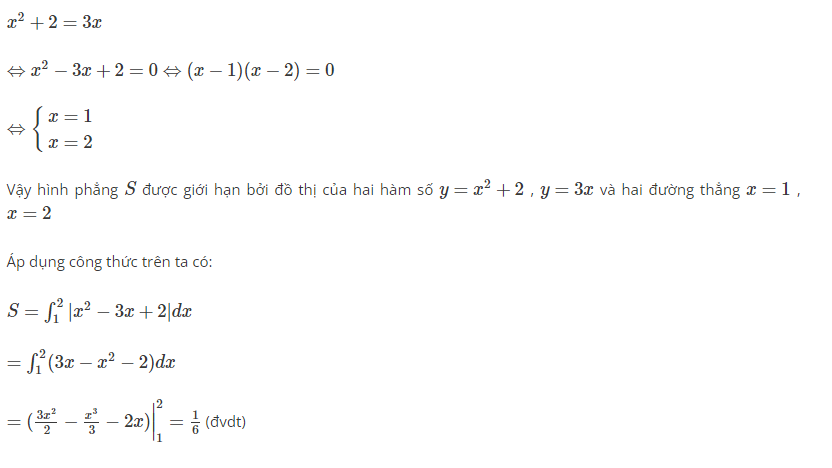
Công thức tính diện tích hình phẳng giới hạn bởi 3 hàm số
Bài toán để ra: Tính diện tích s hình phẳng S được số lượng giới hạn bởi thiết bị thị ba hàm số : y=ƒ(x); y=g(x); y=h(x)
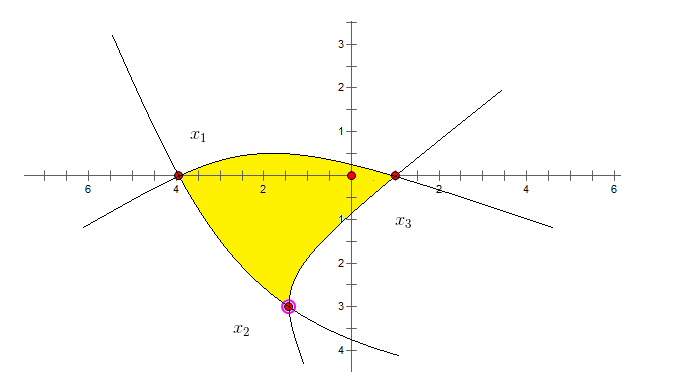
Các cách làm như sau:
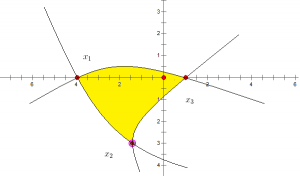
Bước 1: Tìm hoành độ giao điểm của từng cặp đồ thị là x1;x2;x3 với x1 ≤ x2 ≤ x3Bước 2: Diện tích hình phẳng S sẽ được tính theo công thức :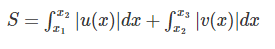
=> trong đó:
Với u(x) là hàm số của phương trình tìm x1v(x) là hàm số của phương trình tìm x2Ví dụ:
Tính diện tích hình phẳng S được số lượng giới hạn bởi cha hàm số : y=3x , y=4−x , y=1
Cách giải:
Ta tìm kiếm hoành độ giao điểm của từng cặp hàm số :
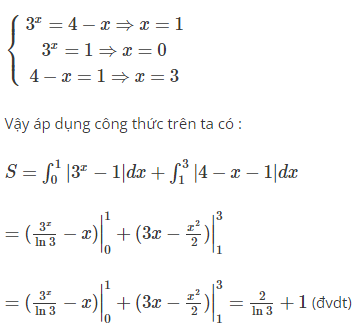
Diện tích hình phẳng giới hạn bởi parabol
Diện tích hình phẳng bị giới hạn bởi parabol và con đường thẳng
– mang đến Parabol y= ax2 + bx + c với b2 − 4ac > 0. Lúc đó diện tích hình phẳng S được số lượng giới hạn bởi vật thị của Parabol cùng với trục hoành được tính như sau:
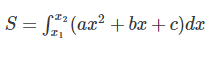
Với x1;x2 là nhì nghiệm của Parabol
Bằng cách chuyển đổi đơn giản thực hiện định lí Vi-ét, từ phương pháp trên ta sẽ có:
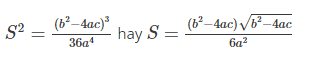
Công thức này thường được áp dụng trong những bài toán trắc nghiệm yêu thương cầu thống kê giám sát nhanh!
Ví dụ:
Tính diện tích s hình phẳng S được giới hản vì Parabol y= x2−5x+6 cùng trục hoành
Cách giải:
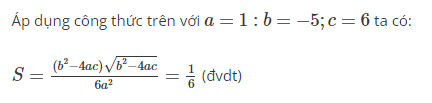
Tính diện tích s hình phẳng số lượng giới hạn bởi parabol và đường tròn
– với dạng toán này , ta đề xuất vẽ hình sơ bộ để dấn diện được hình phẳng phải tính diện tích rồi sau đó sử dụng các công thức cơ bản nêu bên trên để thống kê giám sát thích hợp.
* Chú ý: cùng với dạng bài này khi cần tính tích phân bọn họ sẽ đề xuất sử dụng phương pháp đổi biến chuyển số để tính được tích phân phải tìm.










